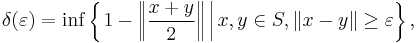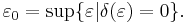Modulus and characteristic of convexity
In mathematics, the modulus and characteristic of convexity are measures of "how convex" the unit ball in a Banach space is. In some sense, the modulus of convexity has the same relationship to the ε-δ definition of uniform convexity as the modulus of continuity does to the ε-δ definition of continuity.
Definitions
The modulus of convexity of a Banach space (X, || ||) is the function δ : [0, 2] → [0, 1] defined by
where S denotes the unit sphere of (X, || ||). The characteristic of convexity of the space (X, || ||) is the number ε0 defined by
These notions are implicit in the general study of uniform convexity by J. A. Clarkson (see below; this is the same paper containing the statements of Clarkson's inequalities). The term "modulus of convexity" appears to be due to M. M. Day (see reference below).
Properties
- The modulus of convexity, δ(ε), is a non-decreasing function of ε. (The modulus of convexity need not itself be a convex function of ε.[1])
- (X, || ||) is a uniformly convex space if and only if its characteristic of convexity ε0 = 0.
- (X, || ||) is a strictly convex space (i.e., the boundary of the unit ball B contains no line segments) if and only if δ(2) = 1.
References
- ^ p. 67 in Lindenstrauss, Joram; Tzafriri, Lior, "Classical Banach spaces. II. Function spaces". Ergebnisse der Mathematik und ihrer Grenzgebiete [Results in Mathematics and Related Areas], 97. Springer-Verlag, Berlin-New York, 1979. x+243 pp.
- Beauzamy, Bernard (1985 [1982]). Introduction to Banach Spaces and their Geometry (Second revised ed.). North-Holland. ISBN 0444864164. MR889253.
- Clarkson, James (1936). "Uniformly convex spaces". Trans. Amer. Math. Soc. (American Mathematical Society) 40 (3): 396–414. doi:10.2307/1989630. JSTOR 1989630.
- Day, Mahlon (1944). "Uniform convexity in factor and conjugate spaces". Ann. Of Math. (2) (Annals of Mathematics) 45 (2): 375–385. doi:10.2307/1969275. JSTOR 1969275.
- Fuster, Enrique Llorens. Some moduli and constants related to metric fixed point theory. Handbook of metric fixed point theory, 133-175, Kluwer Acad. Publ., Dordrecht, 2001. MR1904276
- Lindenstrauss, Joram and Benyamini, Yoav. Geometric nonlinear functional analysis Colloquium publications, 48. American Mathematical Society.
- Vitali D. Milman. Geometric theory of Banach spaces II. Geometry of the unit sphere. Uspechi Mat. Nauk, vol. 26, no. 6, 73-149, 1971; Russian Math. Surveys, v. 26 6, 80-159.
- Pisier, Gilles (1975). "Martingales with values in uniformly convex spaces". Israel J. Math. 20 (3–4): 326–350. doi:10.1007/BF02760337. MR394135. http://www.springerlink.com/content/pwh1126545520581/.